NSSCTF Round#11 Basic

ez_enc

Baconic？No,not baconic

​ 题目已经说了不是培根密码那就不用了，转为二进制就出来了。

EXP

from Crypto.Util.number import *

str = 'ABAABBBAABABAABBABABAABBABAAAABBABABABAAABAAABBAABBBBABBABBABBABABABAABBAABBABAAABBAABBBABABABAAAABBAAABABAABABBABBBABBAAABBBAABABAABBAAAABBBAAAABAABBBAABBABABAABABAAAAABBBBABAABBBBAAAABBBBBAB'.replace('A','0').replace('B','1')

print(long_to_bytes(int(str,2)))

MyMessage

我的消息

​ 题目中已知e并且可以获取多组n、e那就可以使用CRT求解m^{e}了，然后开e次方得到m

EXP

from pwn import *
from Crypto.Util.number import *
from gmpy2 import *
from sympy.ntheory.modular import *

r = remote(IP, Port)
n = []
c = []

e = 127
r.recvuntil(b'Input message')
count = 0
while count != 128:
    r.sendline(b'0')
    out = r.recvuntil(b'Input message')
    n.append(int(out[out.find(b'n: ') + 3:out.find(b'\nToken: ')].decode()))
    c.append(int(out[out.find(b'Token: ') + 9:out.find(b'\nInput messa')].decode(), 16))
    count += 1
    for i in range(len(n) - 1):
        if gcd(n[i], n[-1]) != 1:
            print(n[i], n[-1])
            print(c[i], c[-1])
            exit()
    me = crt(n, c)[0]
    m, f = iroot(me, e)
    if f:
        print(long_to_bytes(m)[1:])
        exit()
    else:
        continue

MyGame

我的游戏

​ 已知n和多组e、c可以使用共模攻击。

EXP

from pwn import *
from Crypto.Util.number import *
from gmpy2 import *


def get_m(n, e1, c1, e2, c2):
    r, s1, s2 = gcdext(e1, e2)  # 计算s1，s2
    m = (pow(c1, s1, n) * pow(c2, s2, n)) % n
    m = long_to_bytes(m)
    return m


r = remote(IP, Port)
n = int(r.recvline().decode()[3:-1])

r.sendline(b'2')
out = r.recvline()
e1 = int(out[7:out.find(b': ')].decode())
c1 = int(out[out.find(b': ') + 2:].decode())
r.sendline(b'2')
out = r.recvline()
e2 = int(out[7:out.find(b': ')].decode())
c2 = int(out[out.find(b': ') + 2:].decode())
r.sendline(b'1')
r.sendline(get_m(n, e1, c1, e2, c2))
print(r.recvline())

ez_signin

App1e_Tree makes a mistake...

​ 观察题目中的num_{1}和num_{2}

通过gcd((num_{1}+num_{2})\% n,n)知道p然后算出q，在已知q、p、e和c后依然无法按照常规的RSA求出m。观察e可发现e=2^{16}且q和p满足4k+3我们便可以用Robin密码系统求出m

EXP

from pwn import *
from Crypto.Util.number import *
from sympy import *

r = remote(IP, Port)
e = 65536
info = r.recv()
num1 = int(info[6:info.find(b'\nnum2')])
num2 = int(info[info.find(b'num2') + 6:info.find(b'\nn=')])
n = int(info[info.find(b'n=') + 3:info.find(b'\nc=')])
c = int(info[info.find(b'c=') + 3:-1])
c_list = [c]
q = gcd(num1 + num2, n)
p = n // q

inv_p = invert(p, q)
inv_q = invert(q, p)

for _ in range(16):
    for c in c_list:
        mp = pow(c, int((p + 1) // 4), int(p))
        mq = pow(c, int((q + 1) // 4), int(q))
        a = (inv_p * p * mq + inv_q * q * mp) % n
        b = n - a
        c = (inv_p * p * mq - inv_q * q * mp) % n
        d = n - c

    c_list = [a, b, c, d]

for i in c_list:
    print(long_to_bytes(i))

ez_fac

App1e_Tree love mathematics.

​ 根据题目中a_{0}^{2}+e×b_{0}^{2}=a_{1}^{2}+e×b_{1}^{2}=n可推e

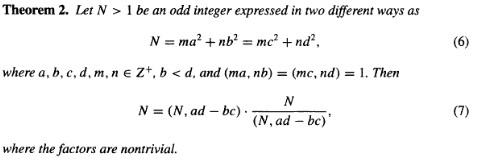
通过上图，求出q，之后便可以正常求解RSA

EXP

from pwn import *
from Crypto.Util.number import *
from sympy import *

r = remote(IP, Port)
info = r.recv()

c = int(info[info.find(b'\nc') + 4:info.find(b'\nn')])
n = int(info[info.find(b'\nn') + 4:info.find(b'\na0')])
a0 = int(info[info.find(b'\na0') + 5:info.find(b'\na1')])
a1 = int(info[info.find(b'\na1') + 5:info.find(b'\nb0')])
b0 = int(info[info.find(b'\nb0') + 5:info.find(b'\nb1')])
b1 = int(info[info.find(b'\nb1') + 5:-1])

e = (pow(a0, 2) - pow(a1, 2)) // (pow(b1, 2) - pow(b0, 2))
q = gcd(n, a0 * b1 - a1 * b0)
p = n // q
phi = (p - 1) * (q - 1)
d = invert(e, phi)
m = pow(c, int(d), n)
print(long_to_bytes(m))

NTR

题目

import gmpy2
from flag import flag
from Crypto.Util.number import *

def init():
    p = getPrime(2048)
    while True:
        x = getRandomNBitInteger(1024)
        y = getPrime(768)
        z = gmpy2.invert(x, p) * y % p
        return (p, x, y, z)

def encrypt(cipher, p, z):
    message = bytes_to_long(cipher)
    r = getRandomNBitInteger(1024)
    c = (r * z + message) % p
    return c

p, x, y, z = init()
c = encrypt(flag, p, z)
with open("cipher.txt", "w") as f:
    f.write("binz = " + str(bin(z)) + "\n")
    f.write("binp = " + str(bin(p)) + "\n")
    f.write("binc = " + str(bin(c)) + "\n")

EXP