《隐私计算》—— 秘密共享
定义
接入结构
定义\{p_{1},\cdots,p_{n}\}为参与方集合,A\subseteq 2^{\{p_{1},\cdots,p_{n}\}}为参与方集合的一个集组。如果集合B\in A且B\subseteq C可推出集合C\in A,那么集组A就是单调的。接入结构定义为\{p_{1},\cdots,p_{n}\}的非空子集的一个单调集组A。接入结构A的内集合被称为授权集合,接入结构A外的集合被称为未授权集合。
秘密域K内的分配方案\sum=<\prod ,\mu>由\prod 和\mu决定。\mu是某个被称为随机字符串集合的有限集合R上的概率分布,\prod是从K\times R到n元组K_{1}\times K_{2}\cdots\times K_{n}的集合的映射,其中,K_{j}被称为秘密份额p_{j}的域。密分发者根据\prod将秘密k\in K分享给各个参与方。首先,密分发者根据采样一个随机字符串r\in R;接着,秘密分发者计算秘密份额向量\prod(k,r)=(s_{1},\cdots,s_{n});最后,秘密分发者安全地将每个秘密份额s_{j}发送给对应参与方p_{j}。
秘密共享
定义K为秘密的有限集合,|K|\leq2。如果以下两个要求成立,那么秘密域K内的分配方案<\prod,\mu>就是实现接入结构A的一个秘密共享方案。
-
正确性:秘密k能够被任何授权的参与方集合恢复。也就是说,对于任何集合B =\{p_{i_{1}},\cdots,p_{i_{|B|}}\}\in A,存在一个恢复函数RECON_{B}:K_{i_{x}}\times\cdots\times K_{i_{|B|}}\to K,对于每个k\in K:
pr[RECON(\prod(k,r)_{B})=k]=1\qquad(2-3) -
隐私保护:未授权的参与方集合不能从它们的秘密共享份额中恢复有关秘密的任何信息。对于任意集合T\notin A,任意两个秘密a,b\in K和任意可能的秘密份额向量<s_{j} >_{p_{j}\in T}:
Pr[\prod(a,r)_{T} =< s_{j} >_{p_{j}\in T}] = Pr[\prod(b,r)_{T}=< s_{j} >_{p_{j}\in T}]\qquad(2-4)注
以上定义要求百分之百的正确性和完美的隐私保护,对于任意两个秘密a、b,分配方案\prod(a,r)_{T} 和\prod(b,r)_T是相同的。我们可以放宽这两个要求:只要求正确性以较高的概率成立,或者\prod(a,r)_{T}和\prod(b,r)_{T}的统计距离很小。符合这两个宽泛要求的秘密共享方案被称为统计秘密共享方案。
秘密共享(替代定义)
如果以下条件成立,那么分配方案是在秘密的给定概率分布S上实现接入结构A的一个秘密共享方案。
-
正确性:对于每个授权集合B\in A
H(S|S_{B})=0\qquad(2-5) -
隐私保护:对于每一个未授权集合T\notin A
H(S|S_{T})=H(S)\qquad(2-6)
以上两种秘密共享方案是等价的,在定理中我们将给出证明。前一定义的好处是,不需要假设一个秘密的概率分布,这个分布是已知的。并且,前一定义能够被泛化成概率秘密共享和计算秘密共享。另外,在证明下限时,后一定义会更加方便。因此,两种定义的等价性使得我们能够为某个特定任务选择更合适的定义。
以上两个秘密共享定义的等价性提供了文献1结果的证明,基于后一定义的秘密共享方案的隐私实际上是独立于分布的:如果秘密共享方案是就秘密的某个分布实现的接入结构,那么在同样条件下,该秘密共享方案可以根据任何分布来实现接入结构。
定理
对于一个秘密分配方案\sum,以下断言是等价的:
- 根据前一定义,秘密分配方案\sum是安全的。
- 在一些支持为K秘密分布(对于任意a\in K,Pr[S=a]>)下,根据后一定义,秘密分配方案是安全的。
- 对于任何支持包含在K中的秘密分布,根据后一定义,秘密分配方案是安全的。
证明
我们先证明定理1可以推出定理3,这样的话,定理1也可以推出定理2。在以下的证明中,\sum=<\prod,\mu>表示一个秘密享方案,其安全性由替代定义提供;S表示一个基于K上某个分布的随机变量,因此,对于任意集合T\notin A,任意密a\in K和任意T中参与方的秘密份额<S_{j}>_{p_{j}\in T}:
式中,S_{T}和S是相互独立的随机变量,根据熵函数的性质,H(S|S_{T})=H(S),因此,根据替代定义,考虑到S上的分布,此秘密共享方案是安全的。
现在,对于支持为K的某个秘密分布,假设\sum=<\prod,\mu>是一个由替代定义设计的秘密共享方案,也就是说,定理2是成立的。那么,对于任意集合T\notin A,随机变量S_{T}和S是独立的,对于任意两个秘密a,b\in K和任意密份额<S_{j}>_{p_{j}}\in T:
第一个和第三个概率是对于固定的秘密来讲的,二者均受到\prod的随机性的影响。第二个则概率同时受到\prod和秘密k的随机性的影响。因此,根据定义,该秘密共享方案是安全的。
原理与实现
秘密共享的发展
- 阈值秘密共享方案
- 一般访问结构上秘密共享方案
- 多重秘密共享方案
- 多秘密共享方案
- 可验证秘密共享方案
- 动态秘密共享方案
- 量子秘密共享方案
- 可视秘密共享方案
- 基于多分辨滤波的秘密共享方案
经典秘密共享方案
Shamir 秘密共享方案
Shamir 秘密共享方案被称作(t,n)门限秘密共享方案2,简称门限方案,t为门限值。Shamir 秘密共享方案是秘密共享中最经典的方案之一,因其简单实用而被广泛应用。Shamir 的方案基于拉格朗日插值的方法实现。给定二维空间内的t个点(x_{1},y_{1}),\cdots,(x_{t},y_{t}),其中x_{i}各不相同。对于每一个x_{i},有且只有一个t-1度多项式q(x)=a_{0} +a_{1}x +\cdots+a_{t-1}x^{t-1},使得q(x_{i})= y_{i}。在秘密拆分阶段,首先要确定t和n。赋值a_{0} = S,S为想要分享的秘密,随机产生a_{1},\cdots,a_{t-1},计算:
获得任意t个S_{i}的值,就可以通过差值法计算得出多项式q(x)的系数a_{0},\cdots,a_{t-1},其中a_{0}为恢复得到的密S。但是,少于t个S_{i}的值不能解出多项式,无法恢复出原本的秘密。为了让上述计算更准确,Shamir 方案用模运算代替实数运算。首先,确定一个大质数p,保证p同时大于S和n,多项式q(x)的系数a_{0},\cdots,a_{t-1}从一个范围为[0,p)的均匀分布中随机取出,且 S_{1},\cdots,S_{n}也通过对p取模得到。下面举一个例子来对 Shamir 密共享方案做进一步的说明。
秘密分发(以t=3举例)
- 假设秘密S,确定n,t,选择模数p
- 生成t-1个小于等于p的随机数a_{1},a_{2},同时将S的值赋给a_{0}
- 分别计算S_{n}=(S+a_{1}\times n+a_{2}\times n^{2})mod\ p
- 将(S_{i},i)作为钥匙分发给第i个人
秘密恢复(以t=3举例)
- 集齐任意t个人的钥匙,例如第一个人的(s_{1},1),第二个人(s_{2},2)和第五个人(s_{5},5)
- 列出方程组a_{o}+i\times a_{1}+i^{2}\times a_{2}mod\ p=S_{i}
- 解出方程组便可得到a_{0}即S
基于中国剩余定理的秘密共享方案
基于中国剩余定理的秘密共享方案设定数据所有者拥有n个数据文件,在加密阶段,算法根据中国剩余定理生成n-1级多项式,利用该多项式对子文件集合中的所有机密文件进行加密,只有授权数据使用者可以访问相应的子文件。在解密阶段中,数据使用者将私有共享和对应的公共共享进行组合,然后恢复该授权使用者想要访问的原始文件或文件集合。
秘密分发(以t=3举例)
-
假设秘密S,确定n,t。
-
生成n个互质的随机数,要求其中的t个最小的随机数相乘的结果大于秘密S,其中t-1个最大的随机数相乘的结果小于秘密S。例如:
d_{1} = 4,d_{2} = 5,d_{3} = 7,d_{4} = 9,d_{5} =11\quad其中d_{1}d_{2}d_{3}>S>d_{4}d_{5} -
分别计算S_{i}=S\ mod\ d_{i}
-
将(S_{i},d_{i})作为钥匙分发给第i个人
秘密恢复(以t=3举例)
- 集齐任意t个人的钥匙,例如第一个人的(s_{1},d_{1}),第二个人(s_{2},d_{2})和第五个人(s_{5},d_{5})
- 列出方程组S\ mod\ d_{n}=S_{n}
- 求解方程组的到S
Brickell 秘密共享方案
Brickel 秘密共享方案是 Shamir 密共享方案的推广,由一维方转向思考多维向量。
密钥分发
-
假设秘密S = 99,确定n =4,向量维度d = 3,选择模数p =127
-
确定解密规则\{(v_{1},v_{2},v_{3}),(v_{1},v_{4})\},其中v_{i}表示第i个d维向量,该解密规则表示第一、二、三个人和第一、四个人分别可以合作恢复出秘密。
-
确定所有人共享的n=4个向量\{v_{1},\cdots,v_{n}\},要求解密规则里的任意一组向量可以线性构成(1,0,0),而不在解密规则里的组合无法构成。例如,v1 =(0,1,0),v2 =(1,0,1),v3 =(0,1,-1),v4=(1,1,0),符合要求:
\begin{aligned} (1,0,0)&=v_{2}+v_{3}-v_{1}\\ (1,0,0)&=v_{4}-v_{1}\\ \end{aligned}\qquad(2-10) -
生成d-1个小于p的随机数,a_{2} = 55,a_{3} =28,同时将S的值赋给a_{1}=99。
-
分别计算S_{i}=a\cdot v_{i}\ mod p,其中a=(a_{1},a_{2},a_{3})
-
将(S_{i},i)作为钥匙分发给第i个人
秘密恢复
-
集齐任意满足解密规则的钥匙,例如第一、二、三个人的为(S_{1}= 55,S_{2}=10,S_{3} =17)。
-
使用第一、二、三个向量构造(1,0,0)
c_{1}v_{1}+c_{2}v_{2}+c_{3}v_{3}=(1,0,0)其参数分别为c_{1}=-1,c_{2}=1,c_{3}=1
-
将参数带入c_{0}S_{i}+c_{2}S_{2}+c_{3}S_{3}=S得到原本秘密S的值
Blakley 秘密共享方案
Blakley 秘密共享方案基于高斯消元法。
密钥分发
-
确定n=5,t=3,假设秘密S=(3,10,5),为t空间中的一点。
-
构造出经过这个点的n =5个平面
\begin{aligned} x+y+z&=18\\ x+y+2z&=23\\ x+y+3z&=28\\ x+2y+z&=28\\ x+3y+z&=38 \end{aligned} -
将第i个平面作为钥匙分发给第i个人。
秘密恢复
-
集齐任意满足解密规则的钥匙,例如第一、二、五个人的钥匙。
-
列出方程组
\begin{aligned} x+y+z&=18\\ x+y+2z&=23\\ x+3y+z&=38 \end{aligned} -
解包含t个变量t个方程的方程组,得到S
秘密共享方案的同态特性
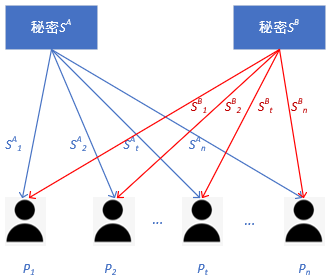
应用最广泛的 Shamir 秘密共享方案,其本身具有加法同态性。假设A、B两方分别有秘密S^{A}和S^{B},如下图所示,他们的值被随机拆分为S^{A}_{1},\cdots,S^{A}_{n}和S_{1}^{B},\cdots,S^{B}_{n},对应被分配到不同节点P_{1},\cdots,P_{n}上,每个节点的运算结果加和可以等同于原始秘密S^{A}和S^{B}的加和。通俗地讲,秘密共享的同态性表达的是:秘密份额的组合等价于组合的秘密共享份额。
同态秘密共享方案允许参与者对接收到的多个子份额进行加乘运算处理,进而在单个秘密处于隐私的状态下即可重构多个秘密的加或乘,因此,秘密共享方案具有同态的性质。对于(t,n)门限秘密共享方案,定义S为原秘密空间,T为秘密份额空间,函数F^{t}\to S把任意t个密份额(S_{i_{1}},\cdots,S_{i_{t}})恢复为原秘密s=F_{I}(S_{i_{1}},\cdots,S_{i_{t}})。其中,I=\{i_{1},\cdots,i_{t}\}\in \{1,2,\cdots,n\},并且|I|=t。
秘密共享同态性
假设\oplus和\otimes分别对应于秘密空间S和份额空间T中的二元函数。(t,n)门限秘密共享具有(\oplus,\otimes)同态性,如果对于任意子集I:
那么
加和同态、乘法同态、除法同态、幂乘同态和比较同态都可以通过对秘密共享方案的设计而实现。
优缺点分析
总的来讲,秘密共享是一种构思巧妙且应用广泛的密码学技术,其优点包括:没有精度损失,相比同态加密的方法,计算效率大大提升,实现相对简单,有很多协议可选,计算成本较低,等等。但是秘密共享也存在一些缺点,例如,在进行线上计算之前必须离线生成并存储许多计算所需的随机数,造成通信成本过高。除此之外,不同的秘密共享方案都有自己的优缺点。
秘密共享优点
t个秘密份额可以确定出整个多项式,并可计算出其他的秘密份额。在原有共享者的秘密份额保持不变的情况下,可以增加新的共享者,只要增加后共享者的总数不超过t即可。还可以在原有共享密钥基础之上,通过构造常数项仍为共享密钥的具有新系数的t次多项式,重新计算新一轮共享者的秘密份额,从而使得共享者原来计算的秘密份额作废。
秘密共享缺点
在秘密分发阶段,不诚实的秘密分发者可将无效的秘密份额分发给参与者。在秘密重构阶段,某些参与者可能提交无效的秘密份额,使得无法恢复正确秘密。秘密分发者与参与者之间需要构建点对点的安全通道。