密码编码学与网络安全——数论基础
2.1 整除性和带余除法
2.1.1 整除性
a, b, m均为整数,存在m使得a = m\times b成立,则称非零数b整除a,表示b|a,同时称b是a的一个因子。
2.1.2 带余除法
任意整数n和任意非整数a,得整数商q和余数r,则满足关系式:
该式称为带余除法。余数r也称剩余数。
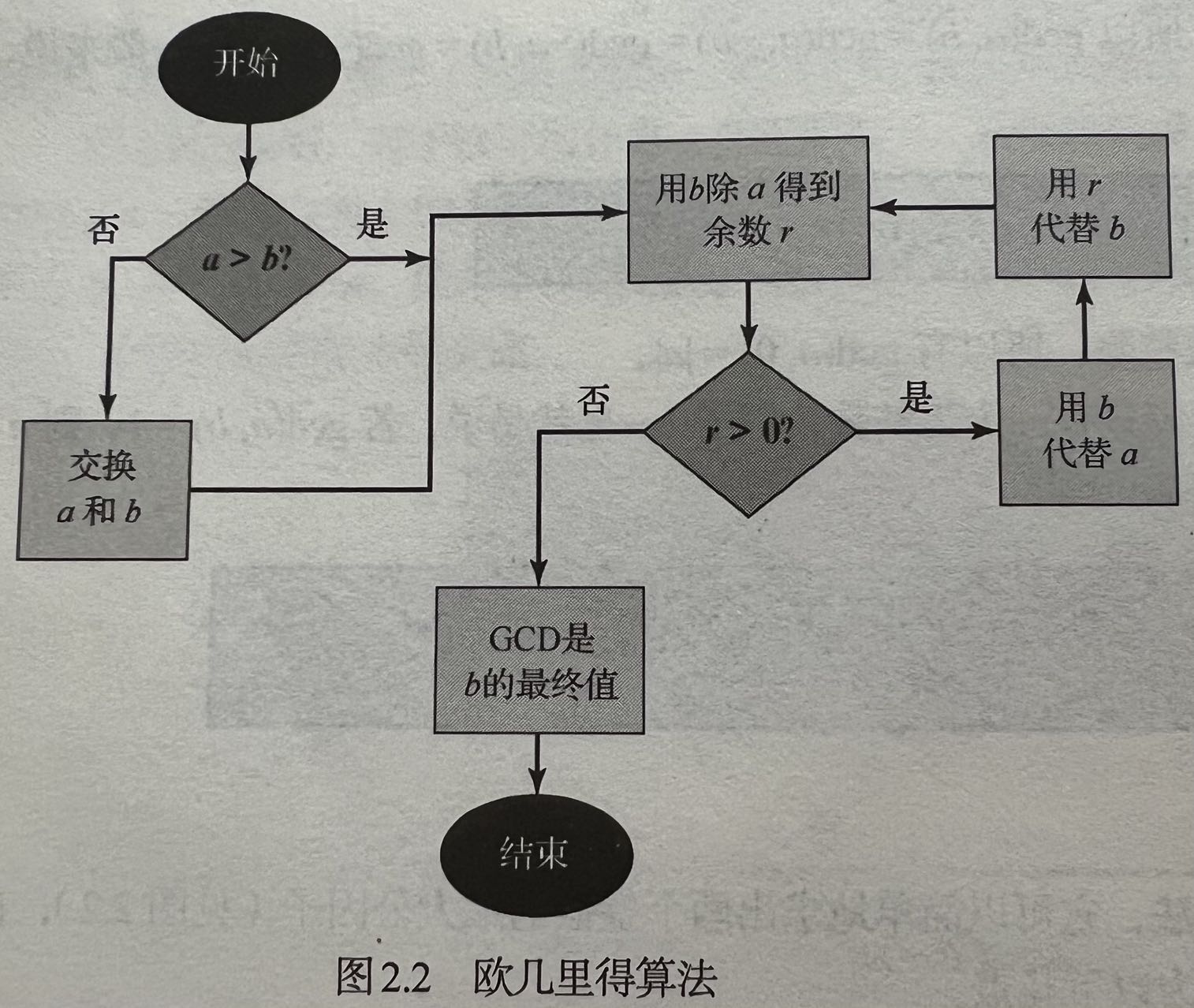
2.2 欧几里得算法
定义:两整数互素,当且仅当它们只有一个正整数公因子1。
2.2.1最大公因子
特殊:\gcd(0, 0) = 0,\gcd(0, n) = |n| 定义:\gcd(a,b) = max[k, 满足 k|a 且 k|b]
2.2.2求最大公因子
-
假设求整数a和b的最大公因子d,即d = \gcd(a, b),因为\gcd(|a|, |b|) = \gcd(a, b),所以这里假定a \ge b > 0。
-
使用带余除法,b除a可以表示
a=q_1*b+r_1,0\le r_1< b\qquad(2.2) -
当 r_{1} = 0时,b整除a,因此d = \gcd(a, b) = b。
-
当r_{1} ≠ 0时,一定有d|r_{1} 。由因子的基本性质可得:存在d|a和d|b,所以一定有d|(a-q_{1}b),即d|r_{1}。
-
对于任意一个b和r_{1}的公因子c ,因为c整除a和b, 所以一定有c \le d 其中d为a和b的最大公因子,因此有d = \gcd(b, r_{1})。 回式(2.2),假设r_{1} ≠ 0,因为b > r_{1},所以可用r_{1} 除b,然后用带余除法得
如上所述,如 r_{2} = 0则d = r_{1};若r_{2} \ne 0则d = \gcd(r_{1}, r_{2})。在计算过程中,余数形成递减的一系列非负值,并且余数为零时算法一定会终止。
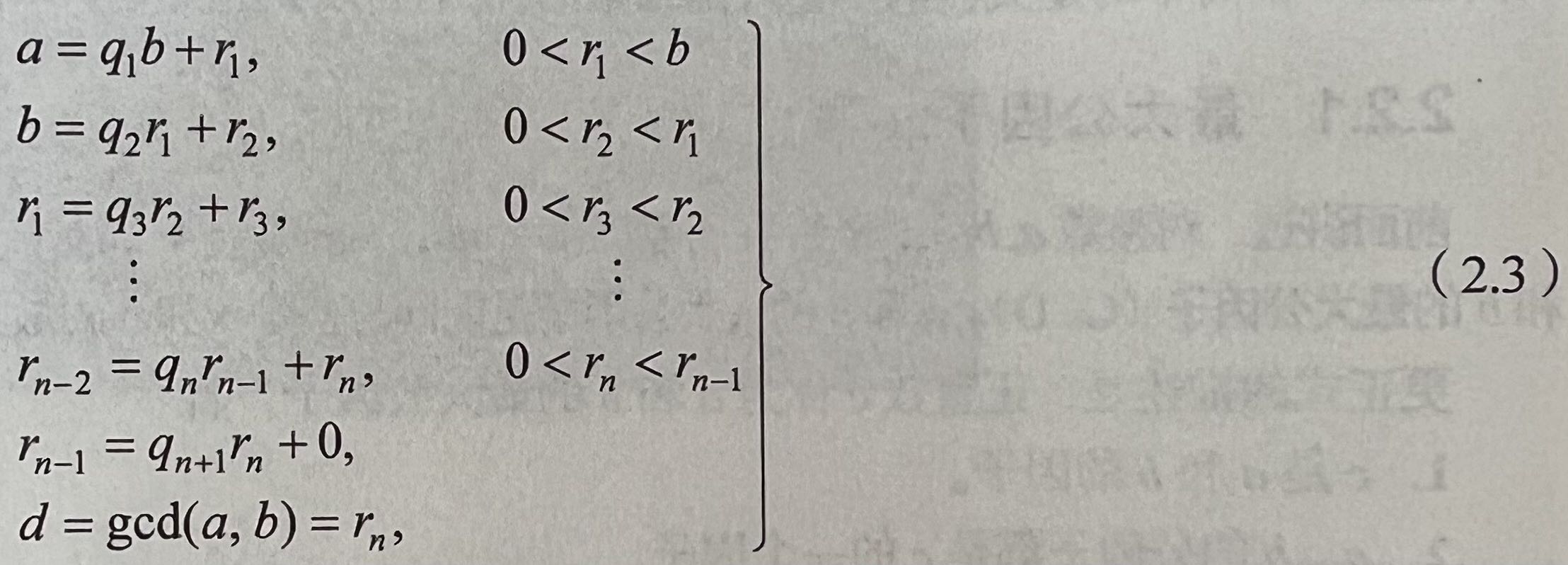
在每次迭代过程中,都进行一次d = \gcd(r_{i}, r_{i-1})运算,直到d = \gcd(r_{n}, 0) = r_{n}。因此可以重复运用带余除法来求两个整数最大公因子,也称欧几里得算法。
2.3 模运算
2.3.1 模
定义整数d除以正整数n所得余数为a模n,n称为模数。
2.3.2 同余性质
- 若n | (a-b),则a \equiv b \pmod{n}
- 若a \equiv b \pmod{n},则b \equiv a \pmod{n}
- 若a \equiv b \pmod{n},b \equiv c \pmod{n},a \equiv c \pmod{n}
2.3.3 模算数运算
- a\%n+b\%n\equiv a+b\pmod{n}
- a\%n-b\%n\equiv a-b\pmod{n}
- a\%n\times b\%n\equiv a\times b\pmod{n}
- 加法逆元:a, b \in Z_{n} ,若(a + b) \% n = 0,则a和b互为加法逆元,记a的加法逆元为-a
- 乘法逆元:a, b \in Z_{n},若(a \times b) \% n = 1,则a和b互为乘法逆元,记a的乘法逆元为a^{-1}
2.3.4 模运算性质
定义比n小的非负数整数集合为Z_{n},
这个集合称为剩余类集,或模n的剩余类。更准确来说Z_{n}中的每一个整数都代表一个剩余类,可将模n的剩余类表示为[0],[1],[2],\cdots,[n-1],其中
寻找与k是模n同余的最小非负数整数的过程称为模n的k约化。
| 性质 | 表达式 |
|---|---|
| 交换律 | w+x\equiv x+w\pmod{n};w \times x\equiv x \times w \pmod{n} |
| 结合律 | (w + x) + y \equiv w + (x + y) \pmod{n};(w \times x)\times y \equiv w×(x × y) \pmod{n} |
| 分配律 | w\times (x + y) \equiv (w \times x) + (w \times y) \pmod{n} |
| 加法逆 | 对每个w \in Z_{n}都存在一个z使得w + z \equiv 0 \pmod{n} |
2.3.6 拓展欧几里得算法
对于给定的a和b采用拓展欧几里得算法计算(x, y, d),按式(2.3)所示的的除法顺序进行计算,并假设每个步骤i都可找到x_{i}和y_{i}满足r_{i} = ax_{i} + by_{i}。最终,得到
| 带余除法 | 假设 |
|---|---|
| a = q_{1}b + r_{1} | r_{1} = ax_{1} + by_{1} |
| b = q_{2}r_{1} + r_{2} | r_{2} = ax_{2} + by_{2} |
| r_{1} = q_{3}r_{2} + r_{3} | r_{3} = ax_{3} + by_{3} |
| ⋮ | ⋮ |
| r_{n−2} = q_{n}r_{n−1} + r_{n} | r_{n} = ax_{n} + by_{n} |
| r_{n−1} = q_{n+1}r_{n} + 0 |
移项得
同样
代入式(2.8)得
然而,前面已假设r_{i} = ax_{i} + by_{i},因此有
总结计算过程如下:
| 计算 | 满足条件 | 计算 | 满足条件 |
|---|---|---|---|
| r_{-1} = a | x_{-1} = 0;y_{-1} = 0 | a = ax_{-1} + by_{-1} | |
| r_{0} = b | x_{0} = 0;y_{0} = 1 | b = ax_{0} + by_{0} | |
| r_{1} = a \% b\\q_{1} = ⌊ a/b ⌋ | a = q_{1}b + r_{1} | x_{1}= x_{-1} - q_{1}x_{0} = 1\\y_{1} = y_{-1} - q_{1}y_{0} = -q_{1} | r_{1} = ax_{1} + by_{1} |
| r_{2} = b \% r_{1}\\q_{2} = ⌊ b/r_{1} ⌋ | b = q_{2}r_{1} + r_{2} | x_{2} = x_{0} - q_{2}x_{1}\\y_{2} = y_{0} - q_{2}y_{1} | r_{2} = ax_{2} + by_{2} |
| r_{3} = r_{1} \% r_{2}\\q_{3} = ⌊ r_{1}/r_{2} ⌋ | r_{1} = q_{3}r_{2} + r_{3} | x_{3} = x_{1} - q_{3}x_{2}\\y_{3} = y_{1} - q_{3}y_{2} | r_{3} = ax_{3} + by_{3} |
| ⋮ | ⋮ | ⋮ | ⋮ |
| r_{n} = r_{n-2} \% r_{n-1}\\q_{n} = ⌊ r_{n-2}/r_{n-1} ⌋ | r_{n-2} = q_{n}r_{n-1} + r_{n} | x_{n}= x_{n-2} - q_{n}x_{n-1}\\y_{n} = y_{n-2} - q_{n}y_{n-1} | r_{n} = ax_{n} + by_{n} |
| r_{n+1} = r_{n-1} \% r_{n} = 0\\q_{n+1} = ⌊ r_{n-1}/r_{n} ⌋ | r_{n-1} = q_{n+1}r_{n} + 0 | d = \gcd(a, b) = r_{n}\\x = x_{n}\\y = y_{n} |
在每一行,基于前两行的余数r_{i-1} 和r_{i-2}计算一个新余数r_{i}。开始这个算法需要r_{0}和r_{-1}有值,他们分别是a和b。而x_{-1},y_{-1},x_{0}和y_{0}的取值则十分的直观。 从原始的欧几里德算法可知,该计算过程会在余数为零时结束,从而求得a和b的最大公因子为d = \gcd(a, b) = r_{n}。与此同时,我们也确定了d = r_{n} = ax_{n} + by_{n}。因此在式(2.7)中,x = x_{n} ,y = y_{n}。
2.4 素数
2.5 费马定理和欧拉定理
2.5.1 费马定理
定理:若p是素数,a \in z^{+},且p|a不成立,则
证明: 考虑小于p的正整数集合\{1,2,\cdots,p-1\},用a乘以集合中的所有元素并对p取模,得到集合X=\{a \% p,2a \% p,\cdots,(p-1)a \% p\}。因为p不能整除a,所以X的元素都不等于0,而且各元素互不相等。为了说明这一点,假设ja \equiv ka \pmod{p},其中1 \le j < k \le p-1,因为a和p互素,因此可将等式[参见式(2.5)]两边的a消去,推出j \equiv k \pmod{p}。这个最后的等式不成立,因为j和k都是小于p的正整数。因此,X的p-1个元素都是正整数且互不相等。所以说X和\{1,2,\cdots,p-1\}的构成相同,只是元素顺序不同。将两个集合的所有元素分别相乘,并对结果模p,有
因为(p-1)!和p互素,根据式(2.5),可以消去(p-1)!这一项,得到式(2.10)。证毕。
费马定理得另一种形式是:若p是素数且a是任意正整数,则
2.5.2 欧拉函数
欧拉函数值小于n且与n互素的正整数的个数。习惯上\phi(1) = 1。对于素数p,有\phi(p) = p-1。假设p和q为素数,p\ne q,那么对n = p\times q有\phi(n) = \phi(p\times q) = \phi(p) \times \phi(q) = (p - 1)\times(q - 1)。 若n = p^{t},其中p为素数,那么\phi(n) = p^{t} - p^{t-1}
2.5.3 欧拉定理
定理:对任意互素的a和$n,有
类似于费马定理,欧拉定理的另一种表述也很有用:
2.6 素性检测
2.6.1 Miller-Rabin算法
素数的两个性质
第一个性质:若p是素数,a是小于p的正整数,则a^{2} \mod p = 1当且仅当a \mod p = 1或a \mod p = -1 \mod p = p - 1。运用模算术运算规则,(a \mod p)(a \mod p) = a^{2} \mod p。因此,若a \mod p = 1或a \mod p = -1,则a^{2} \mod p = 1。反之,若a^{2} \mod p = 1,则(a \mod p)^{2} = 1,其中a \mod p = 1或a \mod p = -1之一成立。 第二个性质叙达如下:设p是大于2的素数,有p - 1 = 2^{k}q,其中k > 0,q为奇数。设a是整数且1 < a < p - 1,则有下面两个条件之一成立:
-
a^{q}模p和1同余,即a^{q} \mod p = 1,或等价地有a^{q} \equiv 1 \pmod{p}。
-
整数a^{q},a^{2q},a^{4q},\cdots,a^{2^{k-1}}中存在一个数,模p时和-1同余。即存在一个j ( 1 \le j \le k)满足a^{2^{j-1}q} \mod p = -1 \mod p = p - 1,或a^{2^{j-1}q} \mod p \equiv -1 \pmod{p}。
算法流程
TEST (n)
- 找出整数k,q,其中k > 0, q是奇数,使n - 1 = 2^{k}q
- 随机选取整数a,1 < a < n - 1
- if a^{q} \mod n=1,then 返回“不确定"
- for j = 0 to k-1 do
- if a^{2^{j}q} \mod n=n-1 then 返回”不确定"
- 返回“合数”
算法实现
import random
# 如果返回值为TRUE表示n为素数,返回值为FALSE表示n为合数。
def MillerRabinPrimeTest(n):
a = random.randint(2, n - 2) # 随机第选取一个a∈[2,n-2]
s = 0 # s为d中的因子2的幂次数。
d = n - 1
while (d & 1) == 0: # 将d中因子2全部提取出来。
s += 1
d >>= 1
x = pow(a, d, n)
for i in range(s): # 进行s次二次探测
newX = pow(x, 2, n)
if newX == 1 and x != 1 and x != n - 1:
return False # 用二次定理的逆否命题,此时n确定为合数。
x = newX
if x != 1: # 用费马小定理的逆否命题判断,此时x=a^(n-1) (mod n),那么n确定为合数。
return False
return True # 用费马小定理的逆命题判断。能经受住考验至此的数,大概率为素数。
# 经过连续特定次数的Miller-Rabin测试后,
# 如果返回值为TRUE表示n为素数,返回值为FALSE表示n为合数。
def isPrimeByMR(n):
if (n & 1) == 0 or n % 5 == 0:
return False
for i in range(100):
if not MillerRabinPrimeTest(n):
return False
return True
#原码链接:https://blog.csdn.net/heshiip/article/details/95679397
2.7 中国剩余定理
表达形式:
式中m_{i}是两两互素的,即1 \le i,j \le k,i \ne j有\gcd(m_{i}, m_{j}) = 1。∀A\in Z_{M},可将A对应于一个k元组(a_{1},a_{2},a_{3},\cdots, a_{k}),即
其中a_{i}有:a_{i} \in Z_{mi}且a_{i} = A \mod m_{i}
CRT说明下列两个断言成立:
-
式(2.15)中的映射是Z_{m}到笛卡尔积Z_{m1} \times Z_{m2} \times \cdots × Z_{mk}的一一对应,也就是说对任何A,0 \le A < M,有唯一的k元组(a_{1},a_{2},a_{3},\cdots,a_{k})与之对应,其中0 \le a_{i} < m_{i},并且对任何这样的k元组(a_{1},a_{2},a_{3},\cdots,a_{k}),Z_{M}中有唯一的A与之对应。
证明:
由A到(a_{1},a_{2},\cdots a_{k})的转换显然是唯一确定的,即只需取a_{i} = A \mod m_{i}。对给定的(a_{1},a_{2},\cdots,a_{k}),可按如下方式计算A。对1 \le i \le k,令M_{i} = \frac{M}{m_{i}},因为M_{i} = m_{1} \times m_{2} \times \cdots \times m_{i-1} \times m_{i+1} \times \cdots \times m_{k},所以对所有j \ne i,有M_{i} = 0 \pmod{m_{j}})。令
c_i=M_i\times(M_i^{-1} mod m_i),\quad 1\le i\le k\qquad\qquad(2.16)根据M_{i}的定义,有M_{i}与m_{i}互素,所以M_{i}有唯一的模m_{i}的乘法逆元,因此式(2.16)是良定的,这样就得到唯一的c_{i}。 计算
A= \begin{pmatrix}\displaystyle\sum_{i=1}^k a_ic_i\end{pmatrix}\pmod M\qquad\qquad(2.17)要证明式(2.17)产生的 A 是正确的,必须证明对1 \le i \le k有a_{i} = A \mod m_{i}。由于i \ne j时c_{j} \equiv M_{j} \equiv 0 \pmod{m_{i}},而且c_{i} \equiv 1 \pmod{m_{i}},故a_{i} = A \mod m_{i}。
-
Z_{M}中元素上的运算等价于对应的人元组上的运算,即在笛卡儿积的每个分量上独立地运算。
2.8 离散对数
2.8.1 模n的整数幂
考虑欧拉定理更一般的表示形式:
若a与n互素,则至少有一个整数m满足式(2.18),即m = \phi(n),我们称使得式(2.18)成立的最小正幂m为下列情形之一:
- a(mod n) 的阶:使得a^{m} \equiv 1 \pmod{n}成立的最小正幂m是a模n的阶
- a所属的模n的指数
- a产生的周期长
我们说\phi(n)是一个数所属的模n的可能的最高指数。若一个数的阶为\phi(n),则称之为n的本原根。本原根的重要之处是,若a是n的本原根,则其幂
是(模 n )各不相同的,且均与n互素。特别地,对素数p,若a是p的本原根,则
是(模 n )各不相同的。素数19的原本根为2,3,10,13,14,15。
并非所有整数都有本原根。事实上,只有形式为2,4,p^{\alpha}和2p^{\alpha}的整数才有本原根,其中p是任何奇素数,\alpha是正整数。
2.8.2 模算术对数
对某个素数p(对非素数亦可)的本原根a,a的1到p - 1的各次幂恰好可以一次产生1到p - 1的每个整数,且只产生一次。而对任何整数b,根据模算术的定义,b满足
因此,对任何整数b和素数p的本原根a,有唯一的幂i使得
该指数i被称为以a为底(模p)的b的离散对数,记为dlog_{a,p}(b)。 注意下列各式:
2.8.3 离散对数的计算
考虑方程
给定y,g,p,计算x(即求离散对数)一般来说是非常困难。已知最快求模数为素数的离散对数的算法的难度级为^{[BETH91]}
但对大素数该算法不可行